Killer Quasiparticles from Space
Cosmic Rays, a serious problem in superconducting quantum computing
One nice thing about working with superconducting qubits is that usually you don’t really have to know much about superconductivity to do the job! Details like the superconducting energy gap of aluminum don’t explicitly enter into most (any?) qubit design considerations and are almost totally irrelevant during normal qubit operations. A quick primer on the Josephson effect, some knowledge of kinetic inductances and capacitances in your fabrication process and you’re off to the races. Newcomers to the field can get pretty far on received superconductivity wisdom and local fabrication knowledge. This remains true as long as the fabrication process is somewhat stable with well-defined rules, and if you’re not trying to make some truly exotic devices.
Sadly, when you do need to know superconductivity, you really need to know it. One such unfortunate circumstance arises when too many quasiparticles are present in the qubits, degrading their performance.
Quasiparticles. One of the most reviled phenomena in the superconducting qubit community. There’s a reason we call it quasiparticle poisoning. Unwanted quasiparticles in Josephson junctions are responsible for a host of ill-effects, most notably causing state relaxation. In other words, quasiparticles can cause our qubits to go from |1⟩ to |0⟩ far sooner than they would normally1.
In general, the low operating temperature (mK) of superconducting qubit devices lends itself to negligible equilibrium populations of quasiparticles. This is why we shouldn’t have to care about them at all. At low temperature, we are able to have high-coherence, long-lifetime devices, which means the Google/IBM/Rigetti QPUs are able to function at all.
Although there is evergreen interest in quasiparticle dynamics, especially in non-equilibrium populations and mitigation strategies, these past few years have resulted in a few papers that specifically investigate quasiparticles in the context of large scale quantum computing.
Specifically, there appears to be concern, backed up by empirical evidence, that cosmic ray showers can generate quasiparticle populations in the substrate of quantum computing chips. These then diffuse outward and cause correlated errors in multiple qubits, which is a major, major problem. Substantial uncorrelated errors would be non-ideal, but able to be overcome with known quantum error correction methods. The surface code, which is the current favorite among error-correction techniques, specifically assumes that errors arise independently. But what about when errors are not independent, because they all occur at the same time and are triggered by the same cosmic ray event? As far as I know, this is major bad news for error correction.
Quasiparticles
So far I’ve been liberally tossing around the word ‘quasiparticles’ without really defining what I mean. If you’re not in the superconductivity business, you may be familiar with some common types of quasiparticles like phonons, plasmons, magnons, etc. Or you may be familiar with the electron (or hole) as a quasiparticle, as in the Fermi sea model of metals.
The situation is a little weirder in superconductors. Quasiparticles2 in a superconductor have contributions from both electrons and holes, and so are often termed “holelike” or “electronlike”. Some quasiparticles can be more electrony than others. This is very strange, and not often explicitly noted. Most experimentalists will just describe quasiparticles in superconductors as electrons and be done with it, but I found Sergey Frolov’s recorded lecture on the subject to be illuminating3.
These quasiparticles in particular display an abundance of rich physics, some of which turns out to be inimical to the error-free operation of quantum computers. As I mentioned earlier, quasiparticles can induce decay in superconducting qubits, effectively crushing what would otherwise be long T1 lifetimes.
Quasiparticle Dynamics
One consequence of unique nature of superconductors is that their quasiparticles, while mostly acting in familiar ways, also have some tricks hidden up their sleeves. Like electrons in normal metals, quasiparticles can move through continuous pieces of superconducting metal. They can move between two pieces of superconducting metal (with a few caveats), and between a superconductor and a normal metal. Electrons can also move from normal metals to superconductors, as long as certain criteria are satisfied.
These facts suggest that qubits can be protected from nearby quasiparticles just by isolating them from other pieces of metal on chip.
This assumption is dead wrong.
Quasiparticles can ‘move’ between two totally unconnected qubits as long as there is some sort of material connection between them. In the case of superconducting qubits, that is usually the silicon wafer substrate on which the qubits are printed.
How can this happen?
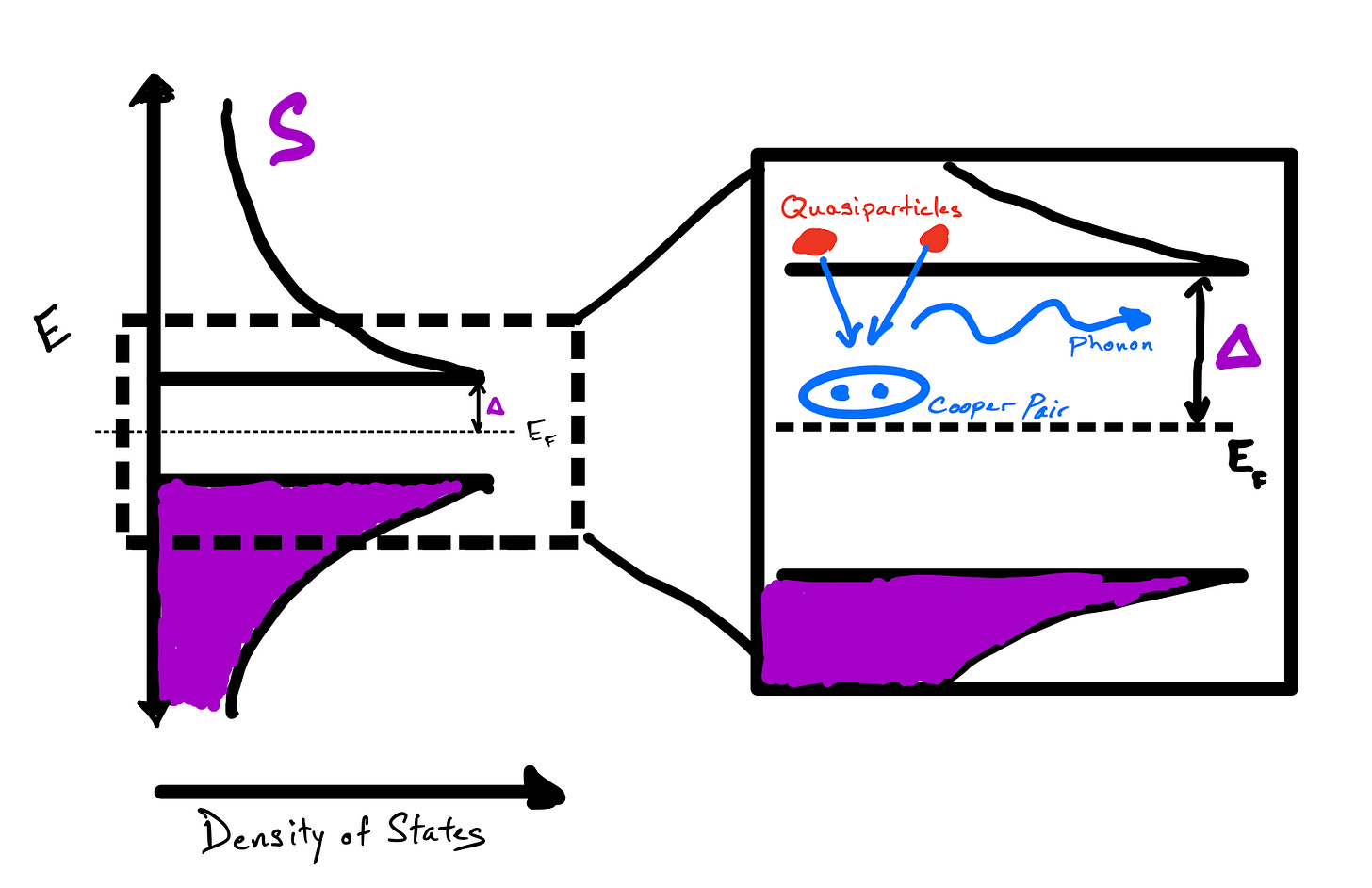
To understand, we’ll need to take a look at the quasiparticle density of states. In the figure below the density of states is plotted on the x-axis, with energy on the y-axis. The dashed line between the two peaks is the Fermi energy of the superconductor, which is also where the Cooper pair condensate is located. The purple coloration indicates filled quasiparticle states up to the edge of the gap.
The distinguishing feature of a superconductor is the so-called “energy gap” that forms between the condensate (dashed line) and the lowest possible quasiparticle excited states. No quasiparticles can exist in this energy gap. We use the symbol Δ to denote the energy gap. So what happens when the lowest energy quasiparticles, with energy Δ, relax back into the Cooper pair condensate? This relaxation happens through a process called ‘recombination’, which requires that two quasiparticles combine to become Cooper pairs and rejoin the ground state. This relaxation emits a phonon with energy 2Δ.
Phonons, unlike electrons, will move freely from metal to insulator and back again. So our pesky quasiparticles, instead of sticking around in a small region of superconductor recombine and blast their energy, in the form of a 2Δ phonon, across the chip! If this phonon enters another superconducting region, like perhaps the Josephson junctions of a far away qubit, it can spend its energy to create two quasiparticles from a Cooper pair in this far-away superconductor.
This key fact about quasiparticles is why they’re so dangerous. Local quasiparticle events very quickly stop being local and can become quite widespread.
Cosmic Rays
So where do cosmic rays come into all of this? The recent paper from the Google quantum team has a great breakdown of events in their Supplementary Materials. You can also read the John Martinis preprint on the same subject, which goes into more detail about the general processes4.
In short:
Muons generated by cosmic ray events in the upper atmosphere smash into the silicon or sapphire substrate of a qubit chip, causing ionization in the silicon wafer.
Most of the charges from 1. recombine and emit photons, but 10-20% will fail to do so and lose energy into the silicon lattice, creating high energy phonons.
Over the next 100 microseconds, phonons travel through the silicon and decay in energy down to ~5 meV. By this point, the phonons could have easily crossed the entire chip multiple times5.
The phonons start breaking Cooper pairs to create quasiparticles6.
Higher energy quasiparticles cool (lose energy) down to Δ, the edge of the gap (see figure above).
Quasiparticles at the gap edge recombine to form a Cooper pair and emit a phonon.
The new phonons either break a new Cooper pair somewhere on chip, repeating step 6, or travel into the wirebonds connecting the chip to the package and are thermalized away in this manner, cooling the chip.
From our knowledge of superconductivity and quasiparticles, we can see how a cosmic ray strike can cause quasiparticle poisoning to spread among many ostensibly “isolated” qubits. Indeed, this is what the Google team observes.
What’s worse is that superconductors with the smallest gaps will act as “traps” for quasiparticles, preferentially accumulating them. Unfortunately, Josephson junctions, a critical component of superconducting qubits, are often made of aluminum, which has a small gap compared to other commonly used superconductors (niobium, indium, tantalum, to name a few).
Quasiparticle Trapping
Why would some superconductors act as traps for quasiparticles? Let’s take a look at the density of states for two different superconductors separated by a thin insulating barrier.
In the figure above I’ve drawn the density of states for two superconductors, one with a larger gap (purple) and one with smaller gap (blue). Let’s pretend these are indium and aluminum, respectively. The purple and blue dots represent quasiparticles with energy exactly equal to Δ1 and Δ2, respectively. We can see that the indium (purple) quasiparticle can easily tunnel into the aluminum, because the edge of the indium gap is higher energy than that of aluminum. That’s another way of saying Δ1 > Δ2. What about the converse, can the aluminum quasiparticle (blue) tunnel into the indium? In this case, no. The aluminum quasiparticles have energy below the superconducting gap edge of indium, and the density of states there is exactly 0. There are no states available for the aluminum quasiparticle to occupy!
Quasiparticle tunneling between two different superconductors can be7 a one way process, from large gap to small gap. This is bad for qubits with aluminum junctions, we don’t want them to collect quasiparticles, after all.
Can we make this work to our advantage?
In principle, yes, by including a sacrificial superconducting metal layer with very small gap. This has been proposed as a mechanism to protect superconducting detectors in astronomy. The Google quantum team could add a thin layer of, say, titanium8 to act as a quasiparticle sponge.
Elsewhere, John Martinis proposes altering standard qubit designs to include small-gap superconductors to act as sponges for quasiparticles as an alternative (or supplement) to an additional global metal layer.
There is one other option. Instead of dealing with finicky superconductors, it is possible to chose a metal with Δ = 0. That is, a metal that doesn’t superconduct at mK temperatures. Two such normal metals are commonly used in low-temperature applications: gold and copper. Since normal metals don’t have a gap, the quasiparticle trapping situation is more straightforward.
Really, normal metals seem to be ideal for this, but there’s a reason you usually don’t see gold or copper on chips with superconducting qubits. Just like it’s easier to put a quasiparticle into a gapless metal, it’s also easier to lose a photon into such a metal. That photon could be our |1⟩ leaving the qubit! In general, metals like gold and copper are considered “lossy” relative to their superconducting bretheren. So if you want to include a normal metal sponge for quasiparticles, there need to be some adjustments made in order to protect the qubits from ‘seeing’ the normal metal. Of course, then there are the proximitization interactions between normal and superconducting metals9.
Where does that leave us?
Based on recent scholarship, we now know that there’s good chance large scale superconducting quantum computers face a “death from above” scenario, where frequent10 cosmic ray strikes interrupt the error-free operation of the QPU and create possibly uncorrectable errors.
However, our knowledge of superconductivity has provided a way out of this situation. As ever, it will require substantial engineering to develop a solution that does not impact qubit quality. Additional mitigation can be provided by shrinking the qubits themselves, so that QC chips take up less space, and, of course, putting the quantum computer a mile or two below the surface of the earth.
Are other qubit types safe?
It’s a little early for the semiconductor and photonics qubit stans to celebrate. From the Martinis paper11:
For semiconductor qubits, the charge offsets produced by silicon electron-hole pairs is as important as the phonon heating discussed here. This prior work shows that significant charge offsets would be seen over large areas (100 µm) for charge-sensitive transmon devices. Will this introduce correlated qubit errors?
Photonic quantum computers are being designed based on superconducting transition detectors [46]. Might the phonon pulse described here be enough to trip these detectors in a way correlated in time and space, and thus detrimental to error correction?
Majorana qubits are made from a special quasiparticle state of a super- and semi-conductor. It would seem that one stray quasiparticle could disrupt this protected state [47, 48]. Is is possible to reduce the quasiparticle number from billions to much less than one so that these states might stay protected?
More generally, will errors from radiation events disrupt any error-correction scheme that does not use many qubits to protect the state? Because radiation events produce non-equilibrium energy pulses of size about 100 µm, are large qubits necessary for errors not to be spatially correlated?
I will conclude with my usual exhortation. There’s still an immense amount of basic science and engineering work to do, gigantic hurdles to leap, etc before quantum computers are able to hit real scale. It’s an exciting time to be in QC!
This isn’t the only effect. Quasiparticles can be responsible for dephasing in qubits as well.
Bogoliubons, if you read M. Tinkham’s Introduction to Superconductivity closely.
Listen from about 18:30 - 27:36.
I focus on muons here, but this can also occur as a result of low(er) energy gamma rays hitting the chip.
The speed of sound in silicon is ~ 5.8 km/s. In the 100 us over which the phonon energy decay occurs, the phonon in silicon would have traveled 580 mm. For comparison, the Sycamore processor chip is 20 mm x 26 mm.
Recall from our figure above that quasiparticles must have energy Δ or greater than the ground state. Here are some common superconducting gaps. Aluminum, Indium, Niobium, and Tantalum are common materials in use in superconducting qubit processes. 5 meV is larger than all gaps presented there.
It doesn’t have to be this way, but such a discussion is outside of the scope of this post.
In the BCS theory of superconductivity, gap size is directly related to superconducting critical temperature (Tc). Metals that superconduct at lower temperatures generally have smaller superconducting gaps. Aluminum superconducts at 1.1 K, while titanium as a Tc between 0.39 - 0.49 K.
It’s tradeoffs all the way down.
The estimates for frequency of cosmic ray strike is reported as 1 ever 38 seconds, and gamma ray events occurred once per 7.6s. These events increase in frequency as the surface area of the target increases.
It’s interesting that John believes that large qubits may be the way to go to reduce correlated error. I’m still bullish on qubit miniaturization and quasiparticle sponges to minimize cosmic ray events, but the optimal solution is clearly far from settled.